Les
Ellipses
I Définition
Une ellipse est l'ensemble des points M du plan dont la somme des distances à
deux points F1 et F2 est constante. MF1+MF2=constante.
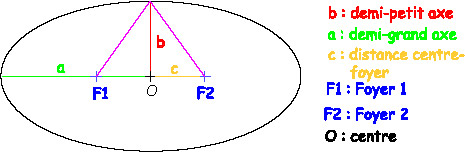
Les points F1 et F2 sont appelés foyers de
l'ellipse.
II Propriétés
Les foyers F1 et F2 sont séparés par une distance égale à
2c, où c est l'excentricité linéaire de l'ellipse. On définit par
ailleurs une longueur a telle que MF1+MF2=2a. a est
appelé le demi grand axe de l'ellipse. Enfin, on définit dans l'ellipse
une longueur b, appelé demi petit axe. On a la relation suivante ( voir
schéma ) : a2=b2+c2. Enfin, il existe une
dernière mesure, appelée excentricité de l'ellipse et notée e, définie
par la relation suivante : e=c/a. e est compris dans l'intervale [0;1[, 0 étant
l'excentricité d'un cercle. Plus e est proche de 1, plus l'ellipse semble
aplatie.
III Equations de l'ellipse
On se place dans un repère orthonormé de centre O.
1) Forme normale, les axes de coordonées coïncident avec les axes de
l'ellipse :
x2/a2+y2/b2=1
2) Forme principale, l'ellipse est en position générale de centre (x0;y0)
(x-x0)2/a2+(y-y0)2/b2=1
3) Représentation paramétrique, de centre (x0;y0) :
x=x0+a*cos(t)
y=y0+b*sin(t)
t appartient à [0;2p]
4) Coordonnées polaires, le pôle au centre de l'ellipse, l'axe polaire étant l'axe [0x) :
r=b/(1-e2*cos2(f))1/2
5) Coordonnées polaires, le pôle au foyer gauche, l'axe polaire étant l'axe [Ox) :
r=p/(1-e*cos(f)) ; p=b2/a
6) Coordonnées polaires, le pôle au foyer droit, l'axe polaire étant l'axe [Ox) :
r=p/(1+e*cos(f)) ; p=b2/a
IV Aire et circonférence de l'ellipse
L'aire A de l'ellipse est définie par la relation suivante : A=pab.
En revanche, la circonférence C de l'ellipse ne peut être représentée de
manière analytique. Elle doit être calculée numériquement par une intégrale. Il
existe cependant des formules d'approximations :
C»p(1.5(a+b)-(ab)1/2)
C»p(a+b)*(64-3L4)/(64-16L2) ; L=(a-b)/(a+b)
V Les coniques.
Enfin, il est bon de dire que les ellipses font partie de la famille des coniques. Les coniques sont des sections planes d'un cône circulaire droit. Si la section coupe toute les génératrices du cône, c'est une ellipse, si elle est parallèle à l'une des génératrices, c'est une parabole, et si elle est parallèle à deux génératrices et coupe les deux moitiés du double cône, c'est une hyperbole. Comme pour l'ellipse, on définit dans les coniques une excentricité. Ainsi, si l'excentricité e est égale à 0, c'est un cercle. Si e est inférieur à 1, c'est une ellipse, si il est égal à 1, c'est une parabole et si il est supérieur à 1, c'est une hyperbole.
L'équation polaire d'une conique revient à celle d'une ellipse, avec le pôle au foyer droit :
r=p/(1+e*cos(f))
où p est le paramètre de la courbe, et e l'excentricité.